As you make progress learning how to play sudoku, you will come across techniques that look similar to ones you have already learned but on your way to becoming an expert sudoku solver, the difference between them will become clearer as you practice.
That is the case with the XY-Wing. In shape, it looks a little like the X-Wing we saw in the last technique post, with a square of cells containing several candidates.
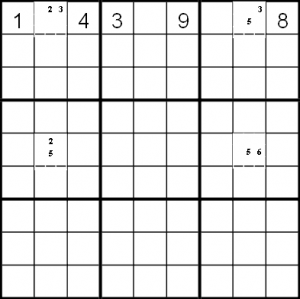
If you look closely at the sets of candidates in 1,2 and in 1,8 and in 5,2 you can see that there are only 3 values shared by the three cells.
If we call them A, B and C, we have a base cell in 1,2 with A and B in it. Then there are two arms (the wings of the Y) which stretch to 5,2 containing A and C and also to 1,8 with B and C in it.
The way this becomes an XY-Wing, rather than just something a bit like a Y is because of the cell at 5,8 to complete the X. In this really simplified diagram, this cell also contains value C as a candidate. Looking at this particular case, it is obvious that C is 5.
If we guess that the entry in 5,8 should really be 5 then it forces the value in 5,2 to be 2 but it also forces the value in 1,8 to be 3. However, that makes it impossible to find a value for the cell 1,2 as it would need to be 3 from the column but 2 from the row.
This clash means that we must have made the wrong assumption about the value 5 in 5,8 and so we can eliminate 5 as a candidate from that cell. In the diagram I have left it as a pair, so we can immediately fill in 5,8 to have the value 6 but this technique will work for any number of candidates in that cell, it is only the 5 that gets eliminated.
This may only clear a single candidate but sometimes this will be the key you need to solve your puzzle.
