Today’s sudoku solving technique came as a revelation to me when I first saw it described. I am aware that I may have been using it unconsciously but it is completely obvious when you see it revealed.
So then, one small step to helping you play sudoku more easily. This is called Naked Pairs. In the same way as we can end up with a naked single, it is possible that we may end up with two cells in a house having exactly the same two values (and no others). You can see this in the grid below.
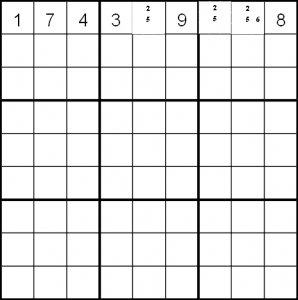
The candidate 2 and 5 exist in both 1,5 and 1,7. Notice that they are also in 1,8 but with 6 as another candidate. Now, what can we say about the possible positions of the 2 and the 5. If 2 is the choice for 1,5 then it cannot be in 1,7 (as we are only allowed one in the row) So 1,7 must be 5. Of course, if 5 were in 1,5 then 1,7 must contain the 2 by the same reasoning. What this means is that we can immediately remove 2 and 5 from the candidates in 1,8 even if we don’t know what order they are really in for those other cells. That leaves us with a naked single 6 which we can enter.
This is fairly easy to see in a row but don’t forget those columns and boxes too. This one technique will move you up the newspaper “hardness” levels and in the next post we will look at the power of naked triples.
