The last technique we looked at can be extended slightly as candidates are exposed more clearly across the grid. In fact there are going to be times when we can’t directly find a new given in a box but we can limit the possibilities for our candidates so that they form a new “line” of influence.
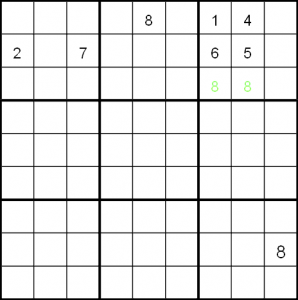
An example will make this clearer. In the diagram, the 8 in 8,9 means that there can be no 8 in that column in box 3. This means that it must be in either 3,7 or 3,8. (Marked in green in box 3) This, in turn, implies that there can be no other 8 in row 3. Looking closer, there must be an 8 in 2,2.
In a related sudoku solving technique called block/block interaction, there are times when two blocks may contain the exact same rows (or colums) containing our candidate. Obviously this does not help if this applies to all three rows, it provides no extra help. However, if just two rows line up, this may help us to eliminate candidates in the third aligned box.
In the case below, 6 can not exist in box 7 in column 2. That means that it has to be in rows 8 or 9 in that box. In the same way, box 8 already has values filling all of row 7 and so 6 must again be in the bottom two rows.
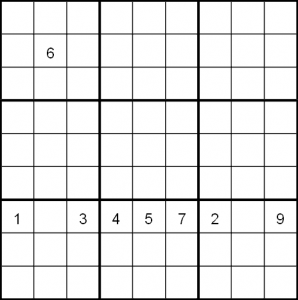
At this point, thinking the situation through, we can say that if 6 is in row 8 in the first box, it must be in row 9 in the second and vice versa – if 6 is in row 9 in the first box, it must be in row 8 in the second. This leads to one of these two situations:
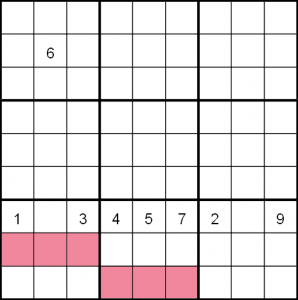
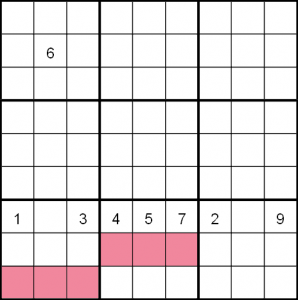
Looking closely, we can see that in both cases, box 9 can not have a 6 in rows 8 or 9 and so there must be a 6 in 7,8
In the next post we will move on to sudoku techniques for the more advanced sudoku solver.

Thanks for these tips, Your final statement in this one throws me though. How did you determine 7,8 from the above? 6 would be in 9,2 but how do we know, yet, about squares 7 or 8?
thanks
Hi kz,
Glad you are finding it useful.
I need to check that you mean the cell references the same way I am using them. So, for me 9,2 means row 9 column 2 and that whole column is excluded because there is already a 6 in it (in 2,2).
So, 7,8 is the far right gap in row 7 that I am looking at. Because the 6 must go in one of the two bottom rows in the bottom-left box (ie box 7) and must also be in the bottom two rows of box 8….there is nowhere else left for it in the final box and so it must go in 7,8.
Does that help? Fire away if I am still not being clear.
Martin
This seems too complicated for me.
By just looking at row 7, cell 7,2 must be 6 or 2. Similarly, cell 7,7 must be 6 or 2.
Since cell 7,2 cannot be 6 (because of 2,2), cell 7,2 must be 2.
So cell 7,7 must be 6.
Maybe your example would have been clearer if you had not colored 8,2 or 9,2.
David, you have me there! I was so busy concentrating on showing the possibilities in boxes 7 and 8 and trying to make it fit the technique, that I completely forgot to say that it is a perfect example of a naked pair. Good catch!