Before we get into the meat of discovering and filling in new numbers in your sudoku grid, I thought it would be worthwhile to go right back to the beginning and describe some of the names used by the real experts of sudoku.I’ll start with what is called “classic” sudoku – we can look at variations some way down the track when everyone has learned all they can about the original. I’ll also fill in the history side of things at a later date.

Classic Sudoku is played on a square grid which is 9 x 9 in size. Usually, these small elements are called cells. Inside the grid, 9 smaller squares of 3 x 3 are marked off and thicker lines indicate the boundaries of these squares, these are sometimes called boxes.
The aim of the game is to fill every row going across, every column vertically and every box with the numbers 1 to 9 without repeating any of those numbers in that row, column or box. So, for example, if you end up trying to put a 3 in a column which already has a 3, you have gone wrong somewhere already!
In fact, it is possible to play sudoku with almost anything in the individual cells. There are variations which use a collection of 9 images instead of numbers. Some people find these to be harder than the numeric version because there is little way to count off the images as you see them.
In order to make it possible to talk to other sudoku solvers about a particular puzzle with a specific combination of numbers, the rows and columns of the grid are assigned numbers. You won’t see these in any published form but the most common approach is to start in the top-left corner for each set as shown below.
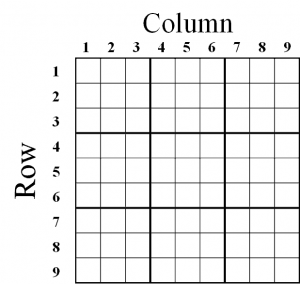
When using this kind of numbering, it is possible to refer to an individual cell and the (almost) universally accepted method is (Row,Column). So, for example, you could talk about an entry being made in cell (2,3) which would be in the 2nd row down and 3rd column across from the left. One additional piece of numbering covers the boxes, which are numbered across from the top, so you have 1,2 and 3 as the top row of boxes, 4,5,6 in the next row etc.
The last piece of naming I am going to cover in this article is for the entries in the cells themselves. When you start a sudoku puzzle, you get a few numbers filled in by the sudoku setter. These are known as “givens”. The number of givens in a puzzle vary enormously – and it is not true to say that a sudoku with a small number of givens is necessarily harder than one with more. However, if you start with more than 40 givens in the grid, it is likely to be a fairly easy puzzle to solve!

The final basic part of the main arsenal for the sudoku solver, is how you go about tracking which numbers could (or could not) go in a particular cell. It is highly likely that you will need to make some kind of marking or annotation on your sudoku which will help you remember where you have been and give you a clearer view of what is available to you. In most cases these are usually pencilmarkings (just to make changes easier). In a large grid with big cells, it is possible to actually write down which numbers are left as possibilities for that cell. These are called candidates and the ideal would be to reduce the number of candidates in each cell to just one possibility, so that you can be sure of being able to fill in that cell.
In this final picture, you can see that 8 is a given in cell (3,5) and that (1,3) has had some entries removed already.
Now that we have some basic naming under our belts, we can move on to looking at some initial sudoku techniques.

I have never seen the Sudoku puzzles with the pictures instead of the numbers. I can imagine they are much harder to keep track of the possibilities.